变频器控制电机电流极限有多大.额定电流?
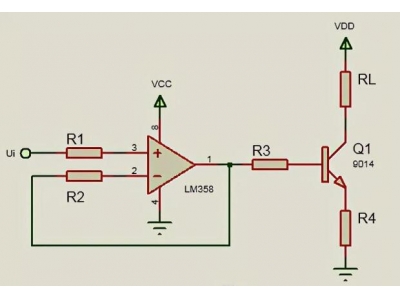
一、变频器控制电机电流极限有多大.额定电流?
变频器驱动三相异步电动机变频器的保护电流,一般是实际是当运行电流,是设置的额定电流的1.2倍,一个小时报过流故障,实际运行电流是1.5倍的设定额定电流时一分钟报过流故障。
不过不同的变频器保护值不一定不同
这就是变频器控制电机电流极限有多大.额定电流的原因
二、变频器极限电流如何设置?
变频器的电流是固定的,这是由变频器的功率所决定的,不可以设置和计算。
因为变频器是应用变频技道术与微电子技术,通回过改变电机工作电源频率方式来控制交流电动机的电力控制设备。变频器主要由整流(交流变直流)、滤波、逆变(直流变交流)、制动单元、驱动单元、检测单元微处理单元等答组成
三、变频器的特点有哪些?
无级调速
2、启动电流小、起动转矩大
3、调速精度高
4、容易实现自动化控制
5、效率高
6、节能型调速 缺点: 1、成本高 2、产生谐波污染电网 3、输出的PWM波,会造成电机、电缆的额外发热、 4、共模电压的产生有可能会降低电机轴的寿命。
四、德力西变频器特点有哪些?
德力西变频器特点论述:
德力西变频器主要运用于电力工业、石油化工、冶金、水资源等工业中的风机、水泵、压缩机等,尤其是应用在高压大功率的风机和泵类机械中,取代传统挡风板、节流阀,可以根据负荷大小适时控制风量和流量,显着提高的节能效果。另外,还可以改善和适应运行环境,平滑加减速、提高加工工艺等功能。
德力西变频器由于采用变频调速后,风机、泵类负载的节能效果最明显,节电率可达到20%~60%,这是因为风机水泵的耗用功率与转速的三次方成比例,当用户需要的平均流量较小时,风机、水泵的转速较低,其节能效果也是十分可观的。而传统的挡板和法门进行流量调节时,耗用功率变化不大。
由于这类负载很多,约占交流电动机总容量的20%~30%,它们的节能就具有非常重要的意义。对于一些在低速运行的恒转矩负载,如传送带等,变频调速也可节能。除此之外,原有调速方式耗能较大者(如绕线转子电动机等),原有调速方式比较庞杂,效率较低者(如龙门刨床等),采用了变频调速后,节能效果也很明显。
五、变频器控制电机电流极限有多大额定电流是35?
变频电机电流比额定电流大,说明电机过流了,也就是过载了,因为变频器的进线功率=变频器出线功率+变频器的损耗,进线电压380V,而频率为35HZ时出线电压是小于380V的,进线电流一定小于出现电流,在变频器为35HZ时,电机所具有的功率不能满足于负载所需,所以在电压不变的情况下,电流就会增加,也就会出现大于电机的额定电流,有时增加频率后,电机所接收的功率能够满足负载所需,因为功率增加,电压增加,电流有时会下降,小于电机的额定电流,不是说频率增加,电机的电流就会增加。
六、丹佛斯变频器电流极限怎么设定?
各变频器进入菜单及菜单模式不一样,常用变频器过载电流设置:
第一步,进入参数菜单,选择“电机电流”项,设置电动机额定电流In第二步,选择“过载保护”项进入一种形式:选择输入过载定值倍率。过载定值倍率范围为100~700%,只需输入100~700间数字即可,变频器会根据设定的额定电流In和过载倍率自动计算后对电机进行过载保护。
另一种形式:选择输入过载电流实际值。即电机额定电流X过载倍率=过载电流实际值第三步:选择过载时间。
七、极限有哪些题型
极限有哪些题型
极限是微积分中非常重要的概念之一。它描述了函数在某一点趋于无穷或趋于某个特定值时的性质。在学习极限的过程中,我们会遇到各种不同类型的题目。本文将介绍一些常见的极限题型,并对每种题型进行详细解析。
1. 基本极限
基本极限是指那些由基本函数组成的极限。基本函数包括常数函数、幂函数、指数函数、对数函数和三角函数等。在求解基本极限时,我们可以运用一些常用的极限公式来简化计算过程。
举例:
- 求解 lim[x→1] (x^2 - 1) / (x - 1)
首先,我们可以将分子进行因式分解,得到:(x + 1)(x - 1)。然后,我们可以约掉(x - 1),最终得到答案为2。
2. 复合函数极限
复合函数极限是指由多个函数构成的函数的极限。在求解复合函数极限时,我们需要运用链式法则和极限的运算法则来化简问题。
举例:
- 求解 lim[x→0] sin(2x) / x
首先,我们可以将 sin(2x) 进行泰勒展开,得到:2x - (2x^3) / 3! + (2x^5) / 5! + ...。然后,我们可以约掉一个x,最终得到答案为2。
3. 无穷极限
无穷极限是指函数在某一点趋于无穷大或无穷小时的极限。求解无穷极限时,我们需要根据函数的性质和极限的定义进行推导。
举例:
- 求解 lim[x→∞] (3x^2 - 2x + 1) / (5x^2 + 3x - 2)
首先,我们可以将分子和分母都除以 x^2,得到:(3 - 2/x + 1/x^2) / (5 + 3/x - 2/x^2)。当 x 趋于无穷大时,2/x 和 1/x^2 的值都趋近于0,因此最终的极限为 3/5。
4. 极限的存在性
在求解极限时,我们还需要关注极限的存在性。有些函数在某一点存在极限,而有些函数则不存在极限。
举例:
- 求解 lim[x→0] 1/x
这个例子中,当 x 趋于0时,1/x 的值会趋近于无穷大或负无穷大,因此这个极限是不存在的。
5. 已知极限求函数值
有时候,我们已知一个函数在某一点的极限,需要求该函数在该点的函数值。求解这类问题时,我们可以运用反函数和极限的运算法则。
举例:
- 求解 f(x) 在 x = 2 处的值,已知 lim[x→2] (f(x) - 4) / (x - 2) = 3
我们可以将等式两边同时乘以 (x - 2),得到:lim[x→2] (f(x) - 4) = 3(x - 2)。然后,我们将两边同时加上4,得到:lim[x→2] f(x) = 3(x - 2) + 4。最终,我们可以将 x 的值代入方程,得到 f(2) 的值。
总结
极限有许多不同的题型,每种题型都需要我们掌握一定的技巧和方法。通过不断的练习和学习,我们可以提高求解极限的能力。希望本文对大家在学习极限题型方面有所帮助,谢谢大家的阅读!
八、极限运算有哪些方法
在数学中,极限运算是一项基本的概念,它在分析学和微积分中扮演着重要的角色。通过极限运算,我们能够研究函数的趋势和性质,解决各种数学问题。本文将介绍一些常见的极限运算方法,帮助读者更好地理解这一概念。
1. 利用代数运算求极限
通过代数运算求极限是一种常用的方法。我们可以利用因式分解、合并分数等代数运算,在不改变极限值的前提下,简化表达式的形式。
2. 利用夹逼准则求极限
夹逼准则是一种重要的极限计算方法。当我们难以直接求得函数值的极限时,可以通过找出两个已知函数之间的关系,将待求极限夹在两者之间,从而确定极限的值。
3. 利用洛必达法则求极限
洛必达法则是一种经典的极限计算方法。当我们遇到形如0/0或无穷大/无穷大的极限时,可以将函数进行导数运算,然后再次求极限,以此逐步逼近最终结果。
4. 利用泰勒展开求极限
泰勒展开是一种将函数在某点附近展开成无穷项幂级数的方法。通过将函数展开成泰勒级数,并截取前几项,我们可以得到函数值的逼近值,进而求得极限的近似解。
5. 利用级数求极限
级数是一种无穷数列求和的表达方式。利用级数求极限是一种常见的数学计算方法。通过将函数展开成级数形式,利用级数收敛性的特点,我们可以得到函数值的极限。
6. 利用积分求极限
积分是微积分中的重要概念,它与极限有着密切的关系。利用积分求极限是一种常见的数学计算方法。通过将函数进行积分运算,我们可以得到函数值的极限。
7. 利用数值近似求极限
当我们无法通过代数运算、夹逼准则或其他方法求得准确的极限值时,可以利用数值近似的方法来计算极限。通过将函数在某一点附近进行计算,可以得到函数值的近似解。
8. 极限运算的应用领域
极限运算在科学、工程、经济学以及其他领域有着广泛的应用。在物理学中,极限运算用于描述物体的运动状态和变化趋势;在工程学中,极限运算用于设计和优化工程结构;在经济学中,极限运算用于分析市场行为和经济趋势。
总结:极限运算是数学中的重要概念,常用于分析函数的性质和解决数学问题。通过代数运算、夹逼准则、洛必达法则、泰勒展开、级数、积分、数值近似等方法,我们可以求得函数的极限值。极限运算在科学、工程、经济学等领域有着广泛的应用,帮助我们更好地理解和解释自然现象和人类活动。
九、新西兰极限游戏有哪些
在新西兰,极限游戏项目丰富多样,吸引着众多喜爱冒险和挑战的游客。不论是高空跳伞、激流漂流还是攀岩等活动,新西兰都为游客提供了许多机会去挑战自我,体验极限运动的刺激与快感。
新西兰极限游戏项目介绍
1. 高空跳伞
新西兰拥有壮丽的自然景观,从空中俯瞰更是一番壮观景象。许多游客选择在新西兰体验高空跳伞,从千米高空跳下,感受飞鸟般的自由。南岛的奎恩斯敦、北岛的陶波湖等地都是极受欢迎的高空跳伞胜地。
2. 激流漂流
新西兰拥有众多湍急河流,适合进行激流漂流活动。游客们可以在激流中尽情体验刺激与挑战,感受急流冲击的快感。新西兰南北岛都有激流漂流项目,例如在奥克兰和怀卡雷的河流。
3. 攀岩
新西兰的巍峨山岩为攀岩爱好者提供了绝佳的场所。从初学者到资深玩家,都可以在这里找到适合自己的攀岩线路。南阿尔卑斯山脉、库克山等地是攀岩的热门场所。
新西兰极限游戏的魅力
新西兰的极限游戏不仅让人体验到刺激与挑战,更让人深刻感受到身心得到释放和放松的感觉。身处自然之中,挑战极限,让人真正感受到生命的激情和活力。
对于喜欢冒险挑战的游客来说,新西兰的极限游戏项目无疑是一个不可错过的体验。在挑战自我极限的同时,还可以领略新西兰壮美的自然风光,让旅行增添更多的乐趣和意义。
结语
新西兰的极限游戏项目丰富多样,无论是高空跳伞、激流漂流还是攀岩等活动,都能让游客感受刺激与快感。体验极限运动,挑战自我,释放压力,是来新西兰旅行的一个绝佳选择。
十、数学有哪些极限问题
数学有哪些极限问题
在数学中,极限是一种非常重要且基础的概念,它涉及到函数、序列等方面,是整个微积分学科中的核心内容之一。那么,数学有哪些极限问题,又有哪些经典的极限定理呢?本文将带领大家一起深入探讨。
1. 函数极限
函数极限是微积分中的一个基本概念,也是最为常见的极限问题之一。当自变量趋于某一特定值时,函数的取值趋于一个确定的值,这个确定的值就是函数在该点的极限值。
对于函数极限的计算,常见的方法有夹逼定理、洛必达法则、泰勒展开等。这些方法在解决各种函数极限问题时发挥着重要的作用,为我们提供了便捷的计算手段。
2. 数列极限
除了函数极限,数学中还有一类与之相关的极限问题,那就是数列极限。数列极限涉及到数学中的序列概念,是研究数列在无穷多项的情况下的极限行为。
常见的数列极限问题包括等比数列的极限、调和数列的极限、斐波那契数列的极限等。这些问题不仅在数学分析中具有重要意义,而且在实际问题中也有着广泛的应用。
3. 多重极限
在数学中,有时候我们需要考虑的不仅是单个变量的极限,还有可能是多个变量的极限,这就是多重极限问题。多重极限涉及到函数在多个变量同时趋于某一点时的极限取值。
对于多重极限的研究,我们常常会遇到二重极限、三重极限等不同情况,需要通过适当的方法和技巧来计算和求解。
4. 极限存在性
在讨论极限问题时,一个重要的问题是极限存在性。也就是说,对于给定的函数或数列,它是否存在极限值,以及如何确定这一极限值。
通过对函数的性质、图像以及极限计算方法的研究,我们可以判断函数的极限是否存在,从而为后续的数学分析工作提供依据。
5. 极限定理
在数学中,有一些经典的极限定理,它们为我们提供了在解决具体极限问题时的重要参考依据。其中比较著名的有夹逼定理、洛必达法则、泰勒展开定理等。
这些极限定理不仅在理论研究中具有重要地位,而且在实际问题求解中也有着广泛的应用。通过运用这些定理,我们可以更加高效地求解各种复杂的极限问题。
结语
总的来说,数学中的极限问题涉及到函数、数列、多重极限等各个方面,是数学分析中一个非常重要的研究内容。通过深入学习和研究极限理论,我们可以更好地理解函数的性质与变化规律,为数学研究和实际问题的分析提供有力支持。
希望本文对大家理解和掌握数学中的极限问题有所帮助,也希望大家能够继续深入学习,探索更多有趣的数学理论。